ACTIVIDAD
6. SUMA Y RESTA DE FRACCIONES
1.1. EXPLICACIÓN
Para ir introduciendo el tema, mira con atención los siguientes videos
SUMA Y RESTA DE
FRACCIONES DE IGUAL DENOMINADOR ( FRACCIONES HOMOGENEAS)
Definición
Suma fracciones con el mismo denominador
Al tener el mismo denominador en las fracciones que vamos a sumar o
restar, dejamos el mismo denominador y sumamos o restamos el numerador.
Vamos a ver un ejemplo. Si sumamos 7/10 y 10/10, dejamos 10 como
denominador de la fracción resultante y sumamos los numeradores, 7 + 10 = 17.
Por lo que el resultado de la fracción sería 17/10.
RESTA DE FRACCIONES CON EL MISMO
DENOMINADOR
La resta de dos ó más fracciones que tienen el
mismo denominador es muy sencilla, sólo hay que restar los numeradores y se
deja el denominador común.
Ejemplo:
SUMA Y RESTA DE FRACCIONES
CON DIFERENTE DENOMINADOR ( FRACCIONES HETEROGENEAS)
SUMA DE FRACCIONES CON
DIFERENTE DENOMINADOR
Multiplicar en
cruz. Se multiplica el numerador
de la primera fraccion por el denominador de la segunda, y el denominador de la
primera por el numerador de la segunda. Ambas multiplicaciones se suman.
Ejemplo:
2. Multiplicar los denominadores
de las dos fracciones. Se multiplican los
denominadores de las dos fracciones.
3. Resolvemos todas las
operaciones.
RESTA DE FRACCIONES CON
DIFERENTE DENOMINADOR
Multiplicar en
cruz. Se multiplica el numerador
de la primera fracción por el denominador de la segunda, y el denominador de la
primera por el numerador de la segunda. Ambas multiplicaciones se restan.
Ejemplo:
2. Multiplicar los
denominadores de las dos fracciones. Se multiplican los denominadores de las dos fracciones.
3. Resolvemos todas las
operaciones.
1.2. AFIANZAMIENTO
Practica lo aprendido:
1.
Resuelve las
siguientes sumas y restas de fracciones homogéneas, practica lo aprendido
2. Resuelve las siguientes sumas y restas de fracciones heterogéneas, practica lo aprendido
1.3. EJERCITACIÓN
Resuelve las páginas 89 en tu libro de trabajo.
ACTIVIDAD 5.
MULTIPLICACION DE FRACCIONES
1.1. EXPLICACIÓN
Para ir introduciendo
el tema, mira con atención los siguientes videos
Escribe en tu cuaderno
el mapa conceptual
MULTIPLICACION Y DIVISION DE FRACCIONES
Definición
LA MULTIPLICACION es muy
sencilla.
La
multiplicación de dos o más fracciones se realiza "en
línea". Es decir, el numerador de la primera fracción por el numerador
de la segunda y el denominador de la primera fracción por el denominador de la
segunda.
Ejemplo
DIVISION DE FRACCIONES
Este método
consiste en multiplicar el numerador de la primera fracción por el denominador
de la segunda fracción y el resultado colocarlo en el numerador de la fracción
final. Por otro lado, tenemos que multiplicar el denominador de la primera
fracción por el numerador de la segunda fracción y el resultado lo
escribimos en el denominador de la fracción final.
Se llama método
de la cruz por el siguiente esquema:
En amarillo: Se
multiplica el numerador de la primera por el denominador de la segunda. El
resultado se escribe en el numerador.
En verde: Se
multiplica el denominador de la primera por el numerador de la segunda. El
resultado se escribe en el denominador.
En el siguiente video entenderás mejor como simplificar fracciones
https://www.youtube.com/watch?v=3HNyVbBNGQQ
1.2.
AFIANZAMIENTO
Practica lo aprendido:
1.
Resuelve las siguientes multiplicaciones
, el resultado dará el nombre del personaje, luego corta y pega si te queda
fácil, de lo contrario identifica los personajes que se ubicarían en el lugar
correspondiente.
2. Resuelve los ejercicios
y encontraras las partes de la trompeta
1.3. EJERCITACIÓN
Resuelve las páginas 91 y 92 en tu libro de trabajo.
Para ir introduciendo el tema, mira con atención el siguiente video.
Fracciones equivalentes
¿Qué son las fracciones equivalentes?
Son aquellas fracciones que representan una misma cantidad, aunque el numerador y el denominador sean diferentes.
Por ejemplo, tenemos dos tortas iguales. De una torta nos comemos medio trozo y de la otra, nos comemos 2 cuartos de torta, ¿en cuál de las dos queda más cantidad de torta?
Hay varias formas. Esta es la manera cómo encontrar fracciones equivalentes usando la tabla de multiplicar.
Observamos la tabla y usamos la primera y segunda fila, coloreadas de azul. Para encontrar una fracción equivalente de un medio nos movemos una columna hacia la derecha y tenemos la misma de antes, dos cuartos
Ahora queremos calcular fracciones equivalentes de tres quintos.
Buscamos la fila del 3 y la del 5. Y nos vamos moviendo hacia la
derecha para encontrar fracciones equivalentes.
Resuelve los siguientes ejercicios para ir practicando.
No debes escribir nada en tu cuaderno.
https://www.cokitos.com/disparar-fracciones-
https://www.cokitos.com/carrera-de-proporciones-equivalentes/play/
Ejercitación
Resuelve la página 86 de tu libro de trabajo.
Explicación
Para ir
introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno
escribe la siguiente información
Tipos de fracciones
Existen 3 tipos de fracciones:
Propias, Impropias y Mixtas. Veamos cada una:
Fracciones propias
Las fracciones propias son aquellas cuyo numerador
es menor que el denominador. Su valor está comprendido entre cero y uno.
Ejemplo:
Fracciones impropias
Las fracciones impropias son aquellas cuyo
numerador es mayor que el denominador. Su valor es mayor que 1.
Ejemplo:
Número mixto
El número mixto o fracción mixta está compuesto de
una parte entera y otra fraccionaria.
Para pasar de número mixto a fracción impropia:
1 Se deja el mismo denominador
2 El numerador se obtiene de la suma
del producto del entero por el denominador más el numerador, del número mixto.
Ejemplo:
Para pasar una fracción impropia a número mixto:
1 Se divide el numerador por el
denominador.
2 El cociente es el entero del
número mixto.
3 El resto es el numerador de la
fracción.
4 El denominador es el mismo que
el de la fracción impropia.
Ejemplo:
Afianzamiento
Practica en el
siguiente link. No debes escribir nada en tu cuaderno.
Ejercitación
Resuelve las páginas 87 y 88
de tu Libro de trabajo.
¡ATENCIÓN!
En el área de Matemáticas, estaremos avanzando en las temáticas relacionadas con los números naturales y sus operaciones. Cada tema tendrá tres fases:
1) Explicación: Donde encontrarás información que te permite comprender la temática. Léela detenidamente porque de esa comprensión depende el desarrollo de las actividades.
2) Afianzamiento: Donde se proponen actividades para afianzar los conocimientos adquiridos.
3) Ejercitación: Donde tendrás la oportunidad de realizar actividades que pondrán a prueba lo que aprendiste.
FRACCIÓN DE UN NÚMERO
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
https://youtu.be/ZNgpSrNEU8E
En tu cuaderno escribe la siguiente información
FRACCION DE UNA CANTIDAD
Para calcular la fracción de una cantidad, se divide la cantidad por el denominador de la fraccón y el resultado se multiplica por el numerador.
Ejemplo
3/6 de 60——————-> 3/6 x60 = ( 60/6 ) x3 =10 x 3 = 30
2/4 de 360 ————-> 2/4 x 360 = ( 360/ 4 ) x 2 = 90 x 2 = 180
Observa la fracción que se indica en cada caso
1/4 de 12 = (12/4 ) x1 3/4 de 16= (16 /4) x3 1/9 de 18 = (18/9 ) x 1
= 3 x 1 = 4 x 3 = 2 x 1
= 3
= 12 = 2
Las estrellas coloreadas Los triángulos azules Corazones coloreados de rojo
Afianzamiento
Practica lo aprendido en los siguientes links
http://ntic.educacion.es/w3//recursos/primaria/matematicas/conmates/actividades/jbc21.htm
Practica lo aprendido
Ejercita tu mente y pon a prueba tus conocimientos
1. Colorea la fraccion que se indica en cada caso y haz la operación
3/5 de 15 3/6 de 24 1/3 de 21
2. Calcula la fracción de cada cantidad, empleando la multiplicación y la división.
Sigue el ejemplo
a) 3/5 de 80 = 3/5 x 80 = 3 x 80 /5 = 240 / 5 = 48
b ) 9/4 de 52 = ————— = —————- = ————- = ———-
c) 10/3 de 60 = ————— = —————- = ————- = ———-
d) 2/5 de 75 = ————— = —————- = ————- = ———-
3. Selecciona la respuesta correcta encerrandola en un circulo en cada una de las siguientes situaciones.
a) Para descansar bien se recomienda dormir la tercera parte del día. ¿Cuántas horas se deben dormir diariamente ?
16 horas 8 horas 10 horas
b) Si Ernesto hace deporte 5/7 de los días de una samana. ¿ Cuántos dias de la semna hace deporte ?
5 días 2 días 7 días
c ) Ana María compró 25 paquetes de galletas para consumir en la semna. Si al final de la semana supo que habia consumudo 3/5 de ellas. ¿ Cuántos paquetes de galletas consumió?.
10 paquetes 15 paquetes 20 paquetes
4. Resuelve: Lee interpreta y soluciona
a) Pablo caminó de la casa al colegio 5/12 de hora. ¿ Durante cuantos minutos caminó Pablo?
b) Pedro cortó 2/5 de una cuerda de alambre de 200 cm. de longitud. ¿Cuánto miden ahora las dos partes de cuerda?
c ) En una granja hay 180 gallinas. Si 3/6 de ellas pusieron huevos. ¿Cuántas gallinas aun faltan por poner?
Ejercitación
Evidencia: Resuelve la página 90 de tu libro de trabajo.
CONCEPTO DE FRACCIÓN
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
https://youtu.be/c9cTIjBqFTw
https://youtu.be/9QM8A-Wz-qA
En tu cuaderno escribe la siguiente información
¿Qué es una fracción?
Definición
Una fracción es un número, que se obtiene de dividir un entero en partes iguales. Por ejemplo cuando decimos una cuarta parte de la torta, estamos dividiendo la torta en cuatro partes y consideramos una de ellas.
Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.
La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.
El numerador es el número de partes que se considera de la unidad o total.
El denominador es el número de partes iguales en que se ha dividido la unidad o total.

Lectura de fracciones
Todas las fracciones reciben un nombre específico, se pueden leer como tal, de acuerdo al numerador y denominador que tengan.
El número que está en el numerador se lee igual, no así el denominador. Cuando el denominador va de 2 a 10, tiene un nombre específico (si es 2 es "medios", si es 3 es "tercios", si es 4 es "cuartos", si es 5 es "quintos", si es 6 es "sextos", si es 7 es "séptimos", si es 8 es "octavos", si es 9 es "novenos", si es 10 es "décimos"), sin embargo, cuando es mayor que 10 se le agrega al número la terminación "avos".
Ejemplos:
En el caso particular de las fracciones con denominador 10 ,100 y 1000.
Ejemplo: 4 se lee " cuatro décimos" , 2 se lee " dos centésimos" y 3 se lee " tres milésimos"
Afianzamiento
Practica lo aprendido en los siguientes links
https://www.thatquiz.org/es-6/?-j1-la-p0
https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/racionales/ejercicios-interactivos-de-fracciones-i.html
https://juegosinfantiles.bosquedefantasias.com/juegos/matematicas/linea-fraccion/index.html
Ejercitación
Evidencia: Resuelve la página 86 en tu libro de trabajo.
MÁXIMO COMÚN DIVISOR
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Máximo común divisor
El máximo común divisor (M.C.D.) de dos o más números es el mayor divisor común de dichos números.
Así podemos encontrarlo.
Afianzamiento
Resuelve los siguientes ejercicios para ir practicando. No debes escribir nada en tu cuaderno.
Ejercitación
Evidencia: Resuelve la página 83 de tu libro de trabajo.
DESCOMPOSICIÓN EN FACTORES PRIMOS
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Descomposición de un número en factores primos
Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.
Para descomponer un número en producto de factores primos se siguen estos pasos:
1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
Ejemplo 1: Realiza la descomposición en producto de factores primos del número 24:
Los números que están a la izquierda de la línea, son los cocientes parciales y los de la derecha, son los factores primos.
Recuerda que siempre debes comenzar por el menor número primo por el cual, el número que te están preguntando, sea divisible.
Ejemplo 2: Realiza la descomposición en producto de factores primos del número 60:
Ejemplo 3: Realiza la descomposición en producto de factores primos del número 180:
Afianzamiento
Resuelve los siguientes ejercicios para ir practicando. No debes escribir nada en tu cuaderno.
http://co.tiching.com/link/11741
Ejercitación
Resuelve la página 79 y 80 de tu libro de trabajo.
Evidencia: Pág 79
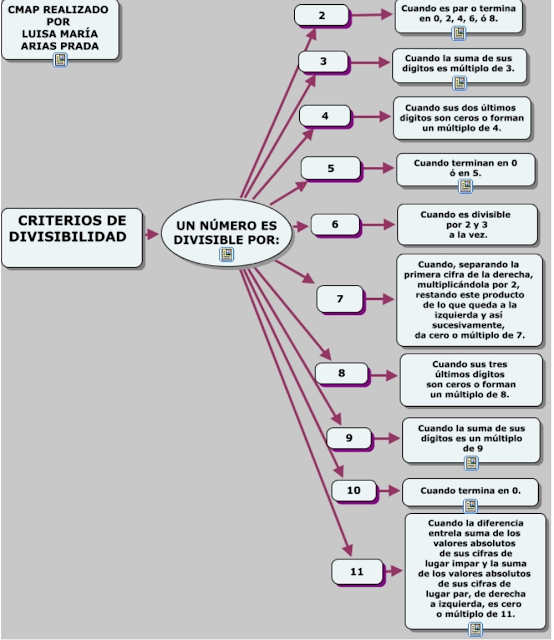
CRITERIOS DE DIVISIBILIDAD
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Criterios de divisibilidad
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división.
Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:
Afianzamiento
Resuelve los siguientes ejercicios para ir practicando. No debes escribir nada en tu cuaderno.
https://www.joaquincarrion.com/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud04/5/05.htm
Ejercitación
Evidencia: Resuelve la página 78 de tu libro de trabajo.
NÚMEROS PRIMOS Y COMPUESTOS
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Números primos y compuestos
Los números primos son aquellos que solo, muy importante, solo son divisibles (al dividirse entre otro da un número entero) entre ellos mismos y el 1.
Por ejemplo: el 7.
Es un número primo porque solo es divisible por 7 y por 1.
Otro ejemplo, el 13 es un número primo. Igual que en el caso anterior, solo lo podemos dividir entre 1 y 13. Además, se puede escribir como la multiplicación de 1×13, pero no como otra multiplicación de números naturales.
Los números compuestos son aquellos que son divisibles por ellos mismos, por la unidad y también por otros números.
Recuerda, el número 1 no se considera ni compuesto ni primo por convenio.
El 25 es un número compuesto. Entonces es divisible por 1, por 25 y por 5. Es decir, 25/25= 1, 25/1= 25 y 25/5=5.
El 14 es un número compuesto y no es primo. Es divisible por 1, por 2, por 7 y por 14. Lo comprobamos: 14/1 = 14, 14/2 = 7 ; 14/7 = 2 y 14/14 = 1.
Estos son los números primos hasta el 1.000
Afianzamiento
Resuelve los siguientes ejercicios para ir practicando. No debes escribir nada en tu cuaderno.
Ejercitación
Evidencia: Resuelve la siguiente actividad en tu cuaderno
DIVISORES
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Los divisores de un número
Los divisores de un número natural son los números naturales que lo pueden dividir, resultando de cociente otro número natural y de resto 0.
Ser divisor es lo recíproco a ser múltiplo. Si 9 es múltiplo de 3, entonces 3 es divisor de 9.
Los divisores de un número natural le pueden dividir, su división es exacta.
Cada número tiene una cantidad concreta de divisores. El número 1 tiene sólo un divisor, él mismo.
Solamente el 0 tiene infinito número de divisores, ya que todos los números son divisores de 0.
Por ejemplo:
D12= {1,2,3,4,6,12}
D30= {1,2,3,5,6,10,15,30}
D8= {1,2,4,8}
En un problema sería lo siguiente:
Afianzamiento
Practica lo aprendido en los siguientes links
http://ntic.educacion.es/w3//recursos/primaria/matematicas/conmates/actividades/jbc21.htm
Ejercitación
Resuelve las páginas 70 y 71 de tu libro de trabajo.
MÍNIMO COMÚN MÚLTIPLO
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
El mínimo común múltiplo de dos números a y b es el número más pequeño que es múltiplo de a y múltiplo de b.
Para denotar el mínimo común múltiplo de a y b escribiremos m.c.m.(a, b) ó mcm(a, b).
Ejemplo:
Vamos a calcular el mínimo común múltiplo de 4 y 6. Para ello, escribimos los primeros múltiplos de 4 y de 6:
Recordad que los múltiplos se obtienen multiplicando.
Entre los 6 primeros múltiplos de 4 y de 6, los números 12 y 24 son múltiplos de ambos (son múltiplos comunes).
Tenemos que quedarnos con el mínimo.
Por tanto, el mínimo común múltiplo de 4 y 6 es 12:
En un problema sería así:
Afianzamiento
Practica lo aprendido en los siguientes links
Ejercitación
Evidencia: Resuelve las páginas 81 y 82 en tu libro de trabajo. Sólo los puntos 1, 2, 3 4 y 6
LOS MÚLTIPLOS DE UN NÚMERO
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
Múltiplos de un número
Los múltiplos de un número se obtienen multiplicando ese número por los números naturales.
- Son múltiplos de 2 los números 0, 2, 4, 6, 8, 10,12, 14... y muchos más.
- Se obtienen al multiplicar 2x0, 2x1, 2x2, 2x3, etc.
- Escribimos así los múltiplos de 2. → m (2) = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.... }
- Son múltiplos de 3 los números 0, 3, 6, 9, 12, 15, 18, 21...
- Se obtienen al multiplicar 3x0, 3x1, 3x2, 3x3, etc.
- Lo escribimos así → m (3) = {0, 3, 6, 9, 12, 15, 18, 21,.... }
¡OBSERVA!
Los múltiplos de un número son infinitos, como infinitos son los números naturales.
Un múltiplo siempre es un número mayor
El número 0 es múltiplo de todos los números (porque al multiplicar cualquier número por cero siempre nos da cero de resultado)... es algo extraño, pero así son las cosas relacionadas con el número 0.
Afianzamiento
Practica en los siguientes enlaces:
https://la.ixl.com/math/6-grado/identificar-los-múltiplos-de-un-número
Resuelve los siguientes ejercicios en tu cuaderno para ir practicando.
Ejercitación
Resuelve las páginas 68 y 69 en tu libro de trabajo.
RADICACIÓN
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
La radicación
La radicación es la operación inversa de la potenciación; es decir si nos dan el área de un cuadrado, extraer la raíz es encontrar el lado de ese cuadrado; mientras que la potenciación nos dan el lado del cuadrado y encontramos el área.
Supongamos que nos dan un número y nos piden calcular otro, tal que, multiplicado por si mismo un número de veces nos da el número.
Por ejemplo: calcular qué número multiplicado por si mismo 2 veces da 196. Ese número es 14. Porque 14 x 14 = 196 → √196 = 14
El número que esta dentro del radical se llama radicando, el grado de la raíz se llama índice y se encuentra en la V del radical, el resultado se llama raíz.
La mejor forma de encontrar las raíces de cualquier número exacto es convertir las raíces a potencias en donde la base de la potenciación es la raíz buscada.
Las raices se llaman según su índice, así:
Para el índice 2 (si el índice es 2, se suele omitir) se le llama raíz cuadrada.
Para índice 3, se llama raíz cúbica; – índice 4, raíz cuarta; – índice 5, raíz quinta, y así sucesivamente, es decir se nombra el número ordinal.
Afianzamiento
Resuelve las siguientes raíces para ir practicando.
Ejercitación
Resuelve las páginas los puntos 1, 2, 3 y 8 de las páginas 74 y 75 en tu libro de trabajo.
EVIDENCIA: Pág 74
LOGARITMACIÓN
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
La logaritmación
Se llaman logaritmo a la potencia que se tiene que elevar en otro número y es llamado base del sistema, se trata en términos generales de un número positivo sirve para obtener el mismo número. Esto es que el logaritmo es el opuesto a la potenciación donde el logaritmo es la potencia.
Obtenemos tres términos que se llaman:
· Base del logaritmo
· Número del logaritmo
· Logaritmo
Así en una potencia:
![]() 5^2= 25
5^2= 25
El cinco se eleva al cuadrado y se obtiene el número 25
Aquí en esta potenciación al pasarla a logaritmo obtenemos lo siguiente:
La base de potencia ahora es la Base del logaritmo = 5
La potencia ahora es el Número del logaritmo = 25
El exponente ahora es el Logaritmo = 2 el cual se coloca en subíndice
Ahora la forma en la que se lee el logaritmo es de la siguiente manera:
Log 5![]() 25 = 2
25 = 2
Se lee Logaritmo en base 5 de 25 = 2
Afianzamiento
Resuelve los siguientes ejercicios para ir practicando.
Ejercitación
Resuelve la página 76 en tu libro de trabajo.
EVIDENCIA:
POTENCIACIÓN
Explicación
Para ir introduciendo el tema, mira con atención el siguiente video.
En tu cuaderno escribe la siguiente información
La potenciación
Las potencias son una manera abreviada de escribir una multiplicación formada por varios números iguales. Son muy útiles para simplificar multiplicaciones donde se repite el mismo número.
Las potencias están formadas por la base y por el exponente. La base es el número que se está multiplicando varias veces y el exponente es el número de veces que se multiplica la base.
¿Qué es la base?
Es el número que se está multiplicando.
¿Qué es el exponente?
Las veces que se repite el número.
¿Cómo se forma una potencia?
Se disponen de la siguiente manera: el número de la base de escribe de forma normal, y el número de la potencia se escribe más pequeño que la base en la parte superior derecha.
Vamos a verlo con el siguiente ejemplo:
5 x 5 x 5 x 5 x 5 x 5 x 5
· ¿Qué número se está multiplicando? El 5, por lo tanto es la BASE
· ¿Cuántas veces se repite el número? 7 veces, por lo tanto es el EXPONENTE
Escribiendo la potencia quedaría así:
Vamos a ver otro ejemplo:
3 x 3 x 3 x 3
· ¿Qué número se está multiplicando? El 3, por lo tanto es la BASE
· ¿Cuántas veces se repite el número? El número se repite 4 veces, por lo tanto es el EXPONENTE
3 x 3 x 3 x 3 = 3 4
Afianzamiento
Resuelve las siguientes potencias para ir practicando.
Ejercitación
Resuelve las páginas 64, 65, 66 y 67 de tu libro de trabajo.
EVIDENCIA: Pág 66 y 67
Orden en las operaciones
El orden correcto a la hora de resolver operaciones es importante. Es necesario resolver cada parte de la operación en el orden adecuado. Este orden o jerarquía a la hora de resolver operaciones combinadas es el siguiente:
- Paréntesis
- Muliplicaciones y divisiones
- Sumas y restas
Lo primero que se debe resolver es aquello que esté dentro de un paréntesis. En caso de que la operación combinada no incluya paréntesis, hay que pasar a lo siguiente en la jerarquía. Después de resolver los paréntesis (o saltarlos si no lo lleva), lo siguiente que debemos hacer es resolver las multiplicaciones (conocer las tablas de multiplicar ayuda) y divisiones, en orden de izquierda a derecha.
Afianzamiento
Escribe en tu cuaderno los siguientes ejemplos.
Vamos a resolver una operación con paréntesis, multiplicaciones, divisiones, sumas y restas.
2+(8×3-6)+4×5-(28:2):2+16=
1. Paréntesis
Primero resolvemos los paréntesis. En caso de haber operaciones diferentes dentro del paréntesis, resolveremos en el siguiente orden: primero multiplicaciones y divisiones, después sumas y restas:
2+(8×3-6)+4×5-(28:2):2+16=
2+(24-6)+4×5-14:2+16=
2+18+4×5-14:2+16=
2. Multiplicaciones y divisiones
Una vez eliminados los paréntesis, lo siguiente que vamos a resolver son las multiplicaciones y las divisiones. En este caso, se resuelven en orden, de izquierda a derecha.
2+18+4×5-14:2+16=
2+18+20-7+16=
3. Sumas y restas
Para terminar, lo último que resolvemos son las sumas y restas. Al igual que en el punto anterior, las resolveremos de izquierda a derecha.
2+18+20-7+16=49
El resultado de la operación sería:
2+(8×3-6)+4×5-(28:2):2+16= 49
Ejercitación
Resuelve en tu cuaderno las siguientes operaciones
RESOLUCIÓN DE PROBLEMAS
Explicación:
Mira el siguiente video
Afianzamiento:
Escribe en tu cuaderno la siguiente información



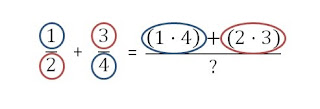




























































profe ya termine lo que nos dijo y lo entendí perfectamente bien ya estoy esperando para que nos diga que hacemos el lunes.
ResponderEliminarATT:ISA
hola profe como estas me hace un favor y me manda el link de los ángulos y muchas gracias
ResponderEliminaratt: tomas amaya
Este comentario ha sido eliminado por el autor.
ResponderEliminar